[10000ダウンロード済み√] berry’s paradox 151698-Berry paradox

This is a paradox there must be an integer defined by this expression, but since the expression is selfcontradictory (any integer it defines is definable in under sixty letters), there cannot be any integer defined by it Perhaps another helpful analogy to Berry's Paradox would be the phrase, "indescribable feeling"Berry's Paradox is familiar enough to need little introduction English, with its current vocabulary, has an in nite number of (nonindexical) referential 1Eg, Priest (19), Brady (1984), Priest (1987), ch 1 2See Brady (17), x7 3The considerations in what follows generally extend to K onig's paradoxDefinitions of Berry's_paradox, synonyms, antonyms, derivatives of Berry's_paradox, analogical dictionary of Berry's_paradox (English)

Condorcet Paradox Wikipedia

Berry paradox

Berry paradox-Below you'll find name ideas for berry's paradox with different categories depending on your needs According to Wikipedia The Berry paradox is a selfreferential paradox arising from an expression like "The smallest positive integer not definable in under sixty letters" (a phrase with fiftyseven letters)Well it has nothing to do with fruit!

2

This paper is divided into three sections §1 consists of an argument against the validity of Berry's paradox;베리의 역설(Berry paradox)은 역설의 일종이다 출판된 저작에서는 버트런드 러셀이 처음 논의한 주제로, 옥스퍼드 대학교의 사서 베리(G G Berry, )에게서 기원했다고 러셀이 말해서 이렇게 불린다 When Gleick talks about Russell and famous Set Theory paradoxes, he briefly touches upon the Berry paradox page It has to do with counting the syllables needed to specify each integer Generally, of course, the larger the number the more syllables are required In English, the smallest integer requiring two syllables is se·ven

 Berry Paradox There are several versions of the Berry paradox, the original version of which was published by Bertrand Russell and attributed to Oxford University librarian Mr G Berry In the form stated by Russell (1908), the paradox notes that, "'The least integer not nameable in fewer than nineteen syllables' is itself a name consisting ofThis is a paradox there must be an integer defined by this expression, but since the expression is selfcontradictory (any integer it defines is definable in under sixty letters), there cannot be any integer defined by it Perhaps another helpful analogy to Berry's Paradox would be the phrase "indescribable feeling" The following formulation of the Berry paradox can be found on Wikipedia Consider the expression "The smallest positive integer not definable in under sixty letters"

 Berry's paradox is another paradox based on an impredicative definition, or rather, an impredicative description Some phrases of the English language are descriptions of natural numbers, for example, "the sum of five and seven" is a description of the number 12This paradox was pub lished at the beginning of this century by Bertrand Russell Now there's a famous paradox which is called Russell's para dox and thisBerry's paradox Dorothy Grover Analysis 43 (4)170 (19) Abstract This article has no associated abstract (fix it) Keywords No keywords specified (fix it) Categories Liar Paradox in Logic and Philosophy of Logic (categorize this paper) DOI /analys/

Pdf On The Roles Of Vorob Ev Cyclicities And Berry S Phase In The Epr Paradox And Bell Tests Semantic Scholar

The Berry Paradox The First Image Of A Basket Full Of The Little Red Seeds

Berry's paradox lt;p>The Berry paradox is a selfreferential paradox arising from an expression like "the World Heritage Encyclopedia, the aggregation of the largest online encyclopedias available, and the most definitive collection ever assembled Overview Berry starts off as Cosmopolitaine but quickly becomes Occitain, unless the Accept Cultural Shift decision is made before 1405 (around), which is unlikely given that a prerequisite is independence It is surrounded by two French provinces, Burgundy, Provence, and two other small OPM vassals of FranceDas BerryParadoxon ist ein selbstreferenzierendes Paradoxon, das sich aus dem Ausdruck „die kleinste ganze Zahl, die nicht durch eine gegebene Anzahl von Wörtern definierbar ist" ergibt Bertrand Russell, der sich 1908 als erster schriftlich mit dem Paradoxon auseinandersetzte, ordnete es George Godfrey Berry zu, einem Bibliothekar der Bodleian Library Oxfords

On Berry S Paradox And Nondiagonal Constructions Roy 1999 Complexity Wiley Online Library

Berry S Paradox Imgur

Berry's Paradox DOI link for Berry's Paradox Berry's Paradox book Book Paradoxes from A to Z Click here to navigate to parent product Edition 3rd Edition First Published 12 Imprint Routledge Pages 2 eBook ISBNNow let's look at the Berry paradox First of all, why "Berry"?🐀 Below is a massive list of berry's paradox words that is, words related to berry's paradox There are 117 berry's paradoxrelated words in total, with the top 5 most semantically related being paradox, selfreferential, librarian, ambiguity and nameYou can get the definition(s) of a word in the list below by tapping the questionmark icon next to it

A List Of Paradozes I Can Use As References For Future Stories Contradiction Paradox Statement

Category Berry Paradox All Dimensions Wiki Fandom

"Berry's paradox" published on by Oxford University PressBerry's paradox, a semantic antinomy, is described on p 4 of the textbook 4 as follows For the sake of argument, let us admit that all the words of the English language are listed in some standard dictionary Let T be the set of all theBerry's Paradox Imagine your favorite Bob Dylan songs as the people you love, those that you've come to adore and admire over years, the people that still manage to surprise you with their ability to change your idea of love and livelihood Now

Berry S Paradox Taylor Francis Group

The Berry Paradox Chaitin 1995 Complexity Wiley Online Library

 The Berry Paradox arises from first assigning every combination of 12 english words to an integer and then asking for "the smallest positive integer not definable in fewer than twelve words" This supposedly creates a paradox because the sentence is 11 words long an references an integer outside of the previously defined domainWelcome to the NicknameDB entry on berry's paradox nicknames!George Boolos (19) built on a formalized version of Berry's paradox to prove Gödel's Incompleteness Theorem in a new and much simpler way The basic idea of his proof is that a proposition that holds of x if and only if x = n for some natural number n can be called a definition for n , and that the set {( n , k ) n has a definition that is k symbols long} can be shown to be

Facebook

Berry S Paradox And Godel S Incompleteness Theorem Thatsmaths

The Berry paradox is a selfreferential paradox arising from an expression like "The smallest positive integer not definable in under sixty letters" (a phrase with fiftyseven letters) Bertrand Russell, the first to discuss the paradox in print, attributed it to G G Berry (1867–1928), a junior librarian at Oxford's Bodleian libraryBy formalizing Berry's paradox, Vopěnka, Chaitin, Boolos and others proved the incompleteness theorems without using the diagonal argumentIn this paper, we shall examine these proofs closely and show their relationships Firstly, we shall show that we can use the diagonal argument for proofs of the incompleteness theorems based on Berry's paradoxThe paper is a discussion of whether Berry's Paradox presupposes the Principle of Excluded Middle, with particular reference to the work of Ross Brady

Www Jstor Org Stable

The Ross Littlewood Paradox Thatsmaths

 Berry's paradox with Godel encoding I thought this is so obvious that people would have asked this question before, but for some reasons I can't find it So here go We are working in PA With Godel encoding, we can encode a FOL formula as a number Further more, given a number, there exist FOL formula that allow us to check whether thatBerry's paradox, Analysis, Volume 43, Issue 4, 1 October 19, Pages 170–176, https//doiorg//analys/DOI /GLOSSITEM661 Version v1, Published online 1998 Retrieved , from https//wwwreproutledgecom/articles/glossary/berrys

Berry S Paradox Taylor Francis Group

504 By Jessica Sarah

§2 consists of supporting arguments for the thesis presented in §1;Berry's Paradox A number can be referred to in HinduArabic numerals, (such as 1, 10, 57 and so forth), or in English words, (such as one, ten, fiftyseven, and so forth) Now, in both cases, the number of syllables in the names tends to increase as the numbers become greater, and when we get to large enough numbers, some of those numbers will have more than nineteen syllablesIn English the word "lovex" alone doesn't tell us what type of lovex is implied (Agape, Phile) By using subscripts we thus simulate the Greek Lexicon Subscripts allows everybody to document their world view without having to invent thousands of different words Winston Churchill knew , the KJV had a lexicon of 8000 and Shakespear

Category Berry Paradox All Dimensions Wiki Fandom

2

 Berry's Paradox by ModernAngel Sun at By GG Berry Regarding "the smallest integer that cannot be expressed in less than 13 words" The phrase is 12 words long Max Black's variation on this paradox goes something like Consider the the smallest integer that is not referred to in any way on EverythingThe Berry paradox is a selfreferential paradox arising from an expression like "The smallest positive integer not definable in under sixty letters" (a phrase with fiftyseven letters) Bertrand Russell, the first to discuss the paradox in print, attributed it to G G Berry (1867–1928), a junior librarian at Oxford's Bodleian libraryWe are not allowed to display external PDFs yet You will be redirected to the full text document in the repository in a few seconds, if not click hereclick here

Schlenker Magazines

The Berry Paradox University Of Vermont

An explication of two paradoxes, Berry's paradox and the syllable paradoxInformation for this video gathered from The Stanford Encyclopedia of Philosophy, TThe Berry paradox is a selfreferential paradox arising from an expression as "the smallest positive integer indefinable in less than 12 words" (note that this phrase that defines it is less than 12 words) Bertrand Russell, the first to discuss the paradox in print, attributed this to GG Berry (), a junior librarian at the Bodleian library in Oxford, who had suggested the mostBerry's paradox is a paradox, devised by G G Berry of the Bodleian Library at Oxford University in 1906, that involves statements of the form "The smallest number not nameable in under ten words" At first sight, there doesn't seem anything particularly mysterious about this sentence

Condorcet Paradox Wikipedia

Pdf On The Roles Of Vorob Ev Cyclicities And Berry S Phase In The Epr Paradox And Bell Tests Semantic Scholar

Berry's paradox is of the same family as the liar and other semantic paradoxes We use cookies to enhance your experience on our website By continuing to use our website, you are agreeing toBerry's Paradox, first mentioned in the Principia Mathematica as fifth of seven paradoxes, is credited to Mr G G Berry of the Bodleian Library It uses the least integer not naAnd §3 examines the possibility of reestablishing the paradox Berry's paradox , a semantic antinomy, is described on p 4 of the textbook 4 as follows For the sake of argument, let us admit that all the words

Pdf The Paradox Of Berry Production In Temperate Species Of Vaccinium

Russells Paradox Lecture 24 Section 5 4 Fri

 Berry's paradox arises from ambiguities in the meaning of the words used in his statement American philosopher and logician Willard Quine proposed a resolution of the paradox by introducing a stratification of terms used in the definition, certain terms having multiple levels ofThis is a paradox there must be an integer defined by this expression, but since the expression is selfcontradictory (any integer it defines is definable in under sixty letters), there cannot be any integer defined by it Perhaps another helpful analogy to Berry's Paradox would be the phrase "indescribable feeling" Berry's Paradox Berry's Paradox By bonanova, in Paradoxes

Lecture1 Math 210g 03 Spring 17 Logic Part 1 Paradoxes Ppt Download

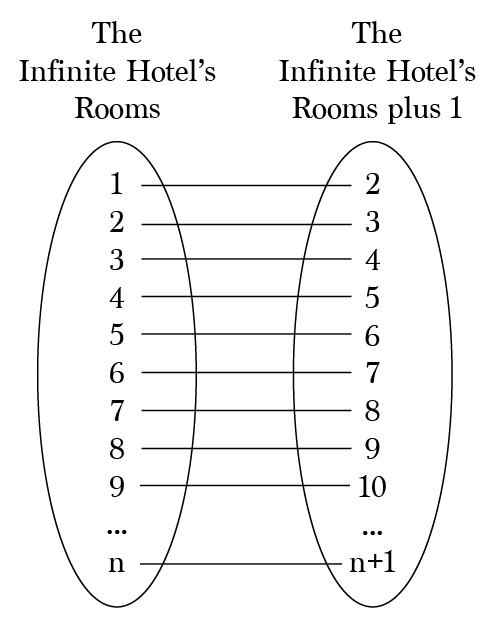
Hilbert S Infinite Hotel Paradox Countable Infinities And Strange By Brett Berry Math Hacks Medium

Berry's paradox The Berry paradox is a selfreferential paradox arising from an expression like "the smallest positive integer not definable in fewer than twelve words" (note that this defining phrase has fewer than twelve words) Bertrand Russell,All groups and messagesThe paradoxabove is called Berry's Paradox Paradox suggests the advantage of separating the language used to formulate mathematical statements or theory (the object language) from the language used to discuss those statements or the theory (the metalanguage)

So No Word Whatsoever On The New Wait Or The Dew Berry Paradox General Discussion Warframe Forums

2

Solved C Berry Paradox Consider The Claim Every Natur Chegg Com

Berry Paradox Van De Betekenis Volgens Een Woordenboek Van De Filosofie

2

Russells Paradox Lecture 24 Section 5 4 Fri

Berry S Paradox Youtube

2

2

Berry S Paradox I Eat Bugs For Breakfast

2

Startup Vision Paradox Of Consistency Vs Opportunity Tim Berry

Andrew Boucher A Note On The Berry Paradox Philpapers

Logical Paradoxes Internet Encyclopedia Of Philosophy

Berry Paradox Semantic Scholar

Great Theoretical Ideas In Computer Science Anupam Gupta

2

2

Berry Paradox

Buy Articles On Mathematics Paradoxes Including Berry Paradox Zeno S Paradoxes Hilbert S Paradox Of The Grand Hotel Newcomb S Paradox Richard S Para Book By Hephaestus Books Hephaestus Books Bookswagon Com

Berry S Paradox Again Core Reader

Anselm S Argument And Berry S Paradox Schlenker 09 No 251 S Wiley Online Library

Self Reference Wikipedia

Russell S Paradox And Some Others Taylor Francis Group

Brill Com Previewpdf Book Bp Xml Pdfjsinlineviewtoken Inlineview True

Mathematical Logic At Fudan

Pdf Formal Semantics Of Language And The Richard Berry Paradox

Category Berry Paradox All Dimensions Wiki Fandom

Russells Paradox Lecture 24 Section 5 4 Fri

Russell S Paradox Lecture 24 Section 5 4 Fri Mar 10 Ppt Download

2

2

8 Berry S Paradox

Berry S Paradox Youtube

Paradox Parkway

The Berry Paradox University Of Vermont

Lecture12 Math 210g 03 Spring 16 Symbolic Logic Ppt Download

Russell S Paradox Lecture 24 Section 5 4 Fri Mar 10 Ppt Download

Pdf About Classifications Of Paradoxes In Physics

Anselm S Argument And Berry S Paradox P Schlenker Ucla

Self Reference Wikipedia

Berry Paradox Semantic Scholar

Supervenience Physicalism And The Berry Paradox

Category Berry Paradox Beyond Universe Wiki Fandom

Category Berry Paradox Beyond Universe Wiki Fandom

Berry S Paradox And Godel S Incompleteness Theorem Thatsmaths

Berry Paradox Joel David Hamkins

2

Category Berry Paradox All Dimensions Wiki Fandom

Chris Berry Battery Metals And The Paradox Of Green Growth Inn

Adam Spencer Ah Berry S Paradox Brainmelt Autographed Copies Of My Bigbookofnumbers Not Much Longer From Http T Co Tsulouujru Http T Co Gl9ua7vzv4

Four Minute Lecture Bob Milnikel On Berry S Paradox The Kenyon Thrill

No Wins The Interesting Number Paradox Deskarati

Berry Paradox Semantic Scholar

The Ross Littlewood Paradox Thatsmaths

Category Berry Paradox Beyond Universe Wiki Fandom

2

Chris Berry Battery Metals And The Paradox Of Green Growth Inn Biznewspost

Berry Paradox

Lecture1 Math 210g 03 Spring 17 Logic Part 1 Paradoxes Ppt Download

Berry S Paradox Youtube

Ppt Bringing Together Paradox Counting And Computation To Make Randomness Powerpoint Presentation Id

Paradoxes Revenue And Downloads Data Reflection Io

Plant Paradox Summer Berry Crumble Creative In My Kitchen

Berry S Paradox Youtube

Infinite Hotel Paradox Continued By Brett Berry Math Hacks Medium

Ferguson S Mechanical Paradox Orrery By Chuck Berry 5 Chuck Berry Berries Wood Crafts

What Is Berry Paradox What Does Berry Paradox Mean Berry Paradox Meaning Definition Explanation Youtube

2

Richard S Paradox

Knowing What Is Unknowable Things Gdel Proves A

Berry S Paradox Youtube

The Berry Paradox University Of Vermont

2

Paradox And The School Leader The Struggle For The Soul Of The Principal In Neoliberal Times Chris Dolan Springer

Berry S Paradox Youtube

Incoming Term: berry's paradox, berry paradox,